Image reconstruction

Image reconstruction in general can be defined as the task of producing an image of an object using several measurements around the object using some sensors. Image reconstruction is quite a broad topic involving different kinds of image formation techniques.

Tomographic reconstruction is one of the most common form of image reconstruction and historically the term was coined for 2D cross-section imaging using X-ray sources and linear array of X-ray detectors. A 3D volumetric imaging can be achieved using 2D planar X-ray detectors.

Forward and inverse problems

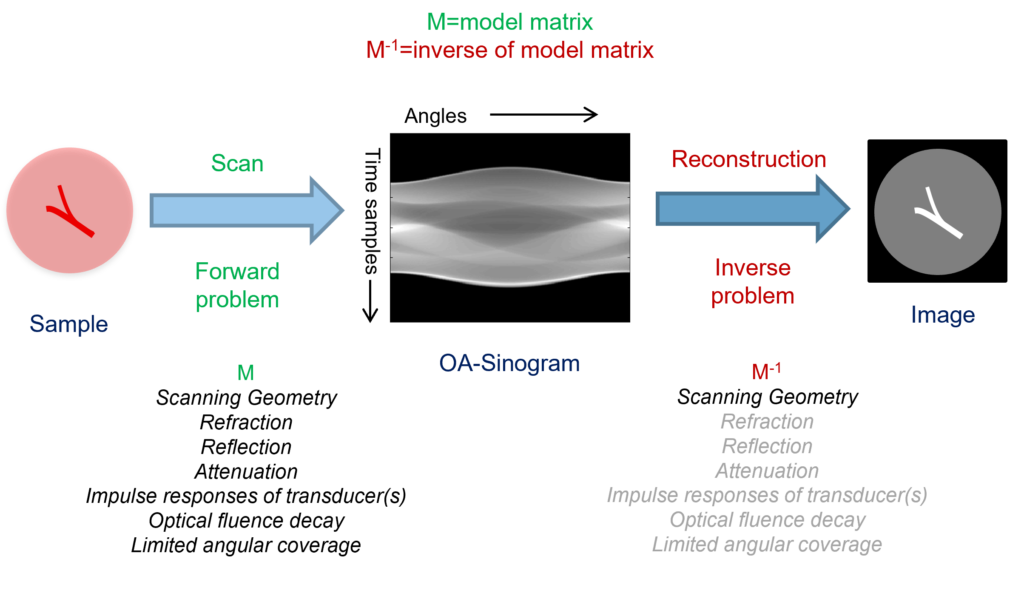
Forward problem defines the formation of sinogram by scanning a sample. Scanning a sample is simply rotating the detector around the sample and capturing projections at different angles. The forward problem captures all physical properties of the imaging process.

The inverse problem defines the reconstruction of the image from the sinogram or the scanned data. The accuracy of the reconstructed results depend on how vividly the physical properties of image formation has been taken into account during the inversion process.

An example of forward and inverse problem in the context of photoacoustic (optoacoustic) image reconstruction is shown in the following figure.

Reconstruction algorithms

  1. Closed form solutions:
    • Backprojection
    • Filtered Backprojection(FBP)
  2. Iterative techniques:
    • Gradient based Algebraic reconstruction techniques:
      • Simultaneous iterative algebraic reconstruction technique (SIRT)
      • Simultaneous algebraic reconstruction technique (SART)
    • Krylov subspace based iterative methods:
      • Conjugate gradient for Least Squares (CGLS)
      • Least square using QR factorization in each iteration (LSQR)
    • Statistical reconstruction methods:
      • Maximum-likelihood expectation maximization (MLEM)
    • Projection onto convex set (POCS) based:
      • Adaptive steepest descent projection onto convex set (ASD-POCS)
    • Proximal gradient based:
      • Chambolle-Pock Primal-dual
      • Adaptive Primal-Dual
      • Iterative Shrinkage-Thresholding Algorithm (ISTA)
      • Fast iterative shrinkage-thresholding algorithm (FISTA)